ABS: A {T} B

STM: p subset wf

ABS: A {T} B

STM: p equiv wf

ABS: T-Detach(A)

STM: detach wf

ABS: detach_fun(T;A)

STM: detach fun wf

STM: detach fun properties

STM: exists det fun

STM: exists det fun a

STM: dec alt char

STM: dec alt char a

ABS: E <>{T} E'

STM: binrel eqv wf

STM: binrel eqv transitivity

STM: binrel eqv weakening

STM: binrel eqv inversion

STM: binrel eqv functionality wrt breqv

ABS: E >{T} E'

STM: binrel le wf

STM: binrel le antisymmetry

STM: binrel le transitivity

STM: binrel le weakening

ABS: x,y:T. E(x;y)

STM: ab binrel wf

STM: ab binrel functionality

ABS: a [r] b

STM: binrel ap wf

STM: binrel ap functionality wrt breqv

ABS: dec_binrel(T;r)

STM: dec binrel wf

ABS: refl(T;E)

STM: xxrefl wf

STM: xxrefl functionality wrt breqv

ABS: sym(T;E)

STM: xxsym wf

STM: xxsym functionality wrt breqv

ABS: trans(T;E)

STM: xxtrans wf

STM: xxtrans functionality wrt breqv

ABS: xxsymmetrize(E)

STM: xxsymmetrize wf

ABS: irrefl(T;R)

STM: xxirrefl wf

ABS: anti_sym(T;R)

STM: xxanti sym wf

STM: xxanti sym functionality wrt breqv

ABS: st_anti_sym(T;R)

STM: xxst anti sym wf

ABS: connex(T;R)

STM: xxconnex wf

STM: xxconnex functionality wrt breqv

ABS: order(T;R)

STM: xxorder wf

ABS: EquivRel(T;R)

STM: xxequiv rel wf

STM: xxorder functionality wrt breqv

STM: xxorder eq order

ABS: xxlinorder(T;R)

STM: xxlinorder wf

ABS: E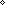

STM: refl cl wf

ABS: E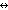

STM: sym cl wf

ABS: E\

STM: s part wf

STM: s part functionality wrt breqv

STM: s part char

STM: xxorder split

STM: xxtrans imp sp trans

STM: refl cl is order

STM: irrefl trans imp sasym

STM: xxconnex iff trichot

STM: xxconnex iff trichot a

STM: rel le refl cl sp

STM: refl cl sp le rel

STM: refl cl sp cancel

STM: rel le sp refl cl

STM: sp refl cl le rel

STM: sp refl cl cancel

ABS: Ident(T;op;id)

STM: ident wf

STM: sq stable ident

ABS: Assoc(T;op)

STM: assoc wf

STM: sq stable assoc

ABS: Comm(T;op)

STM: comm wf

STM: sq stable comm

ABS: Inverse(T;op;id;inv)

STM: inverse wf

STM: sq stable inverse

ABS: BiLinear(T;pl;tm)

STM: bilinear wf

STM: sq stable bilinear

STM: bilinear comm elim

ABS: IsBilinear(A;B;C;+a;+b;+c;f)

STM: bilinear p wf

STM: sq stable bilinear p

ABS: IsAction(A;x;e;S;f)

STM: action p wf

STM: sq stable action p

ABS: Dist1op2opLR(A;1op;2op)

STM: dist 1op 2op lr wf

STM: sq stable dist 1op 2op lr

ABS: fun_thru_1op(A;B;opa;opb;f)

STM: fun thru 1op wf

STM: sq stable fun thru 1op

ABS: FunThru2op(A;B;opa;opb;f)

STM: fun thru 2op wf

STM: sq stable fun thru 2op

ABS: Cancel(T;S;op)

STM: cancel wf

STM: sq stable cancel

ABS: monot(T;x,y.R(x;y);f)

STM: monot wf

STM: sq stable monot

STM: monot functionality

ABS: monotone(T;T';x,y.R(x;y);x,y.R'(x;y);f)

STM: monotone wf

ABS: RelsIso(T;T';x,y.R(x;y);x,y.R'(x;y);f)

STM: rels iso wf

STM: assoc shift

STM: comm shift

STM: cancel shift

STM: eqfun p shift

STM: sym shift

STM: trans shift

STM: connex shift

STM: anti sym shift

STM: refl shift

STM: monot shift

Up

Algebra